Verwendete Mathematik
die Mathematik ist nicht zu schwer
Unser größtest Defizit des Menschen ist seine Unfähigkeit, die exponentielle Funktion zu verstehen. (Prof. Al Bartlett)
Exponentielle Probleme sind schwer für unseren Verstand zu begreifen, weil wir eher linear statt exponentiell denken.
Die Mathematik zur Analyse des Coronavirus-Ausbruchs ist nicht zu schwierig. Die angewendeten Modelle für die Datenfits und Vorhersagen sind erstaunlich einfache Modelle, in denen nur wenige Parameter angepaßt werden müssen, um verhältnismäßig genaue Aussagen zu erhalten. In einigen Modellen sind Parameter nicht umabhängig genug, um mit der Methode der kleinsten Fehlerquadrate angepaßt zu werden.
Ihre Unterstützung wird uns helfen, die Datenanlyse zu Covid-19 für Sie fortzusetzen:

(Wenn Sie auf das Bild klicken, akzeptieren Sie Cookies vom Drittanbieter, die von Paypal benötigt werden.)
Exponential growth
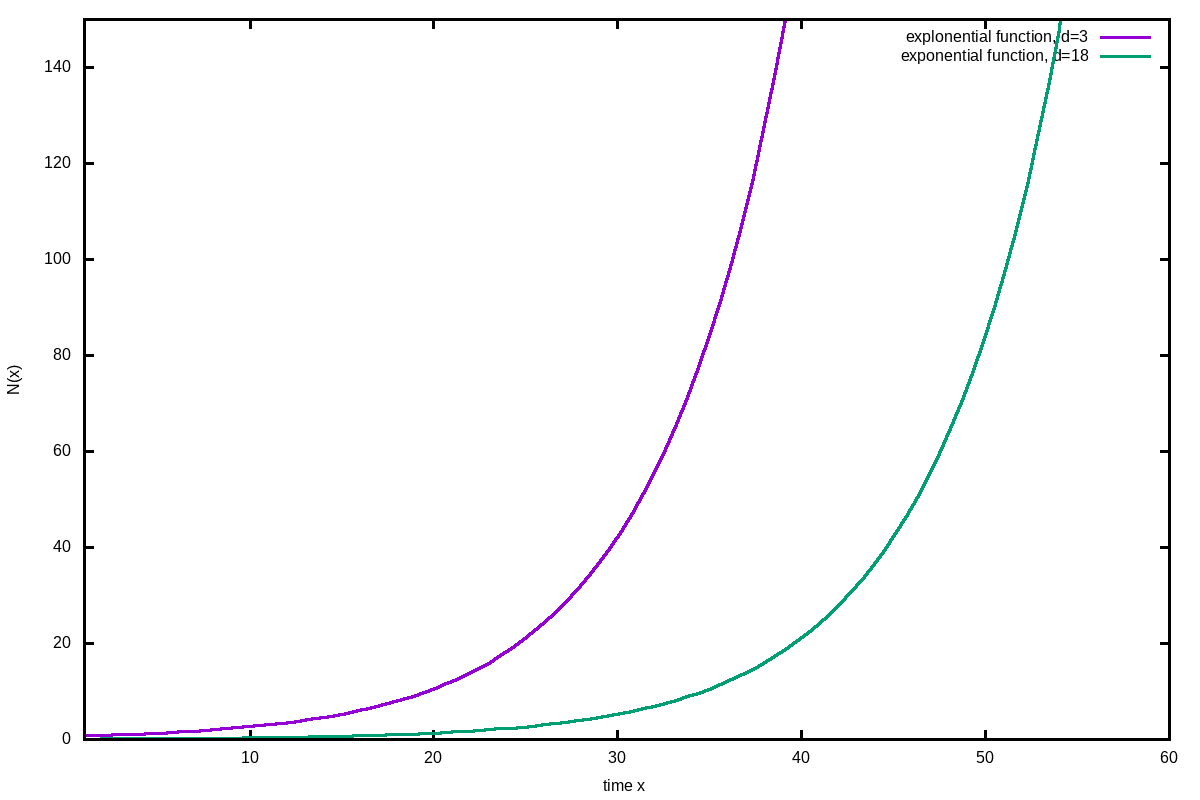
Ein sehr einfaches Wachstumsmodell ohne Begrenzung ist:
\[ N(x) = N_0\cdot e^{\frac{ln(2)}{T_2} (x-d)} \]
Dabei ist:
e: Eulersche Zahl 2.71828182845905…
N0: Zahl der Organismen am Anfang bei der Zeit Null
N(x): Zahl bei der Zeit x
x: die Zeiteinheit, die Sekunden, Minuten, Stunden, Tage, Jahre betragen kann
d: die Verschiebung der Fuktion entlang der x-Achse mit Zeiteinheit d
T2: die Verdopplungszeit von N(x).
In realen Daten liegt der Startpunkt möglicherweise nicht bei Null. Daher muss die Funktion entlang der x-Achse verschoben werden, ohne dass sich ihre Form ändert, was durch den Parameter d erreicht wird. Wenn d positiv ist, verschiebt sich die Funktion nach rechts. N0 und d sind jedoch nicht vollständig unabhängig und verursachen Probleme, wenn Daten nach der Methode der kleinsten Quadrate angepasst werden. Das Ergebnis sind sehr große Fehlerwerte. Daher kann nur einer dieser Werte angepasst werden und der andere erfordert eine gute Schätzung. Wenn in den meisten Fällen N0 bekannt ist, kann der Beginn eines Wachstums berechnet werden, z. Wenn N0 = 1 ist, dann überschreitet N(x) den Wert 1, (x-d) gibt die Zeit an.
Diese einfache Funktion ist besonders zu Beginn eines natürlichen Wachstums nützlich, wenn keine Einschränkungen das Wachstum behindern. Der wichtigste Wert, den wir erhalten, ist die Verdopplungszeit, die die Wachstumsgeschwindigkeit angibt.
Verdopplungszeiten sind nützlich, um einfache Kopfrechnungen durchzuführen:
\[ N = N_0\cdot 2\cdot 2\cdot 2\cdot 2 … \]
oder
\[ N = N_0 \cdot 2^n \]
mit n der Zahl der Verdopplungen. Um die Zeit für die Verdopplungen zu berechnen, gilt:
\[ time = T_2 \cdot n \]
Diese einfache Mathematik kann leicht ohne Taschenrechner durchgeführt werden. Es zeigt vereinfacht, wie schnell die Zahlen steigen können. Nehmen wir ein praktisches Beispiel und nehmen wir an, dass die Verdopplungszeit T2 = 3 Tage ist und wir n = 32 verdoppeln, indem wir N0 = 1 verdoppeln. Die Zahl N ist:
\[ N = 1 \cdot 2^{32} = 4,294,967,296 \]
Dies wäre etwas mehr als die Hälfte der Weltbevölkerung in 32 Schritten. Die nächste Verdoppelung, als 33 Schritte insgesamt, wird bereits doppelt so hoch sein. Wie lange wird es dauern:
\[ time = 3 \cdot 32\ days = 96\ days \]
Es dauerte ungefähr 3 Monate, um die Hälfte der Bevölkerung zu erreichen. Wie lange dauert es, bis die Hälfte der Bevölkerung die gesamte Bevölkerung erreicht: 1 Verdopplungszeit: 3 Tage!
Wenn wir davon ausgehen, dass 0,2% der Bevölkerung infiziert sind, bleibt dann noch viel Zeit, bis alle betroffen sind? Die Antwort ist ungefähr 9 Verdopplungszeiten oder ungefähr 4 Wochen.
Wann ist es an der Zeit, auf exponentielle Wachstumsprobleme zu reagieren? Am Anfang!
Logistische Funktion
Die einfache exponentielle Wachstumsfunktion kann nur zu Beginn eines Wachstumsprozesses verwendet
werden. Unter natürlichen Bedingungen ist die Anzahl möglicher erweiterbarer Räume oder Opfer von
Viren begrenzt. Wenn die Begrenzung zu wirken beginnt, wird die Expansion verlangsamt und nähert sich
der Begrenzung. Es kann beschrieben werden durch:
Dabei sind die Variablen dieselben wie beim einfachen exponentiellen Wachstum und es kommen noch hinzu:
Nmax: maximales N, das möglich ist.
Die Funktion hat die Form einer symmetrischen S-Form. Die Verdopplungszeit T2 zeigt den Anstieg am Anfang und die asymptotische Annäherung am Ende. Während des Übergangs gibt es eine charakteristische lineare Phase mit einem Wendepunkt.
Sobald der Wendepunkt überschritten ist, können Anpassungen ziemlich genaue Nmax-Ergebnisse liefern. In der Realität haben natürliche Wachstumsprozesse jedoch unterschiedliche Formen und eine längere abnehmende Phase ist häufig zu beobachten. Daher sollte diese Funktion am Anfang nur als erweiterte Ersetzung der einfachen Exponentialfunktion in Problemen verwendet werden, da wir Nmax mit einer realistischen Grenze festsetzen können, um so eine bessere Vorhersage für die nächsten Tage zu erhalten.
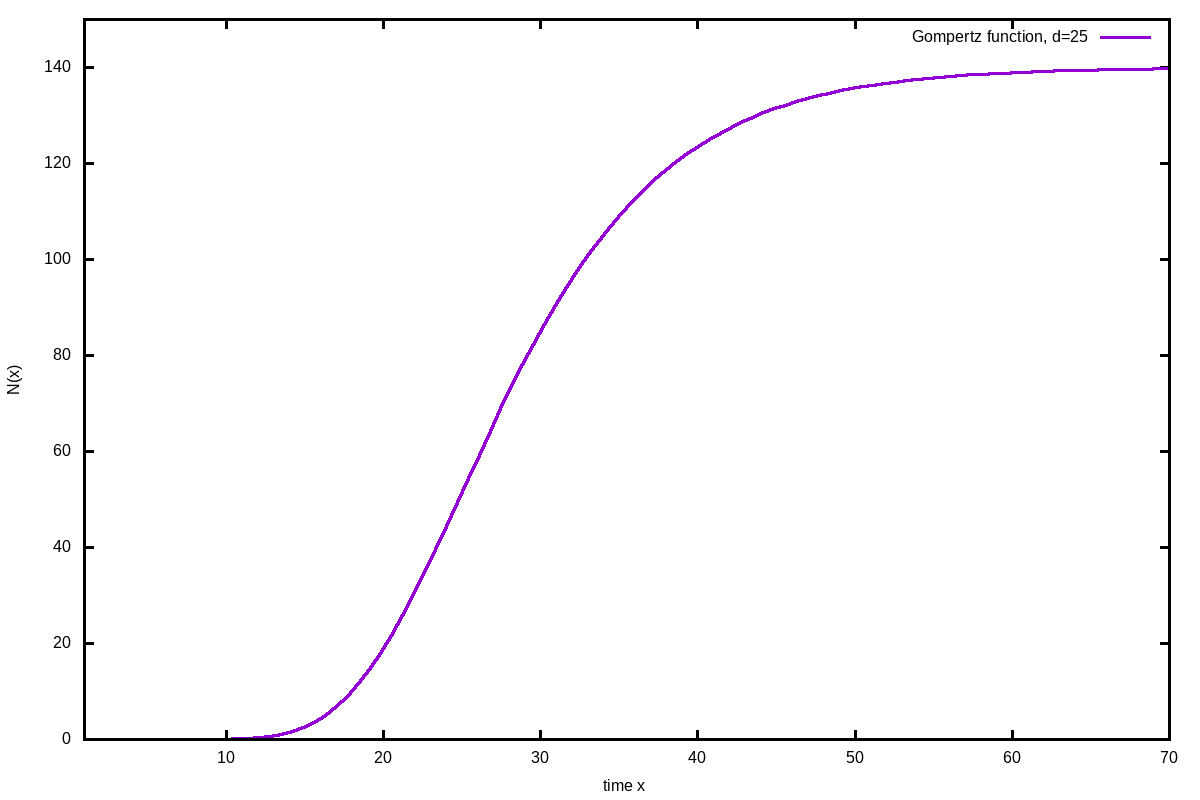
Gompertz function
Benjamin Gompertz has described a double exponential formula to describe naturally observed growths:
\[ N(x) = N_{max}\cdot e^{-b\cdot e^{-c\cdot x}} \]
Hierbei sind:
b: Verschiebung entlang der x-Achse (abstrakter Wert)
c: Wachstumsrate (abstrakter Wert)
Mittlerweile werden viele Variationen dieser Formel verwendet, die in der folgenden Literatur beschrieben sind.
Wenn Sie diese Formel für die Anpassung verwenden, führt die Matrix der kleinsten Quadrate auch zu großen Fehlerwerten, da b und c im Exponenten nicht so unabhängig voneinander sind, wie erforderlich wäre. Daher habe ich Formeln in eine vereinfachte Version umgewandelt, die sehr robuste Anpassungen mit aussagekräftigen Ergebnissen liefert:
\[ N(x) = N_{max}\cdot e^{-e^{-ln(2)/T_2\cdot (x-d)}} \]
Dabei ist:
Nmax: Die asymptotisch maximale Zahl der Wachstumsfälle
T2: die Verdopplungszeit im Wendepunkt
d: die direkte Zeit des Wendepunktes!
Wir haben daher sehr wichtige Variablen, um den Wachstumsprozess zu bewerten. Besonders wichtig ist der Zeitpunkt des Wendepunkts, da er uns sagt, wann z.B. eine Epidemie wieder unter Kontrolle ist. Erst nach dem Wendepunkt wird die Anzahl der täglichen Neuinfektionen geringer. Bis zum Ende des Prozesses bleibt jedoch noch viel Zeit, da wir am Wendepunkt nur etwa 37% der Infektionen in der Funktion erreicht haben! Schlimmer noch, am Wendepunkt ist nur ungefähr 20% der Zeit bis zum Ende vergangen.
T2 beschreibt die Verdopplungszeit am Wendepunkt und ziemlich gut auch die asymptotische Annäherungszeit. Der einzige Nachteil dieser Funktion ist, dass sie nicht die Verdopplungszeit zu Beginn dieses Wachstums angibt. Moderne Versionen mit zwei Verdopplungszeiten bieten keine stabilen Fits. Daher wird auf dieser Website diese modifizierte einfache Form verwendet. Wie gut es das Wachstum beschreibt, kann an den Ebola-Daten untersucht werden. Dort sehen Sie auch die beiden unterschiedlichen Verdopplungszeiten im ersten und zweiten Teil, die mit der Logistischen Funktion angepasst wurden, aber jeweils nur auf den Wendepunkt beschränkt sind.
Diese modifizierte Gompertz-Funktion ist zu Beginn eines Wachstums nicht sehr genau, wenn wir weit vom Wendepunkt entfernt sind. Sie ist sehr empfindlich gegenüber kleinen Änderungen. Das Fehlen einer Verdopplungszeit in dieser frühen Phase kann zu einer Fehlinterpretation führen, insbesondere sollte T2 nicht mit der Verdopplungszeit in der Phase des schnellen Anstiegs verwechselt werden. In dieser Phase wird die Verwendung der Logistikfunktion empfohlen, die jedoch hier Nmax überschätzen kann. Sobald wir uns dem Wendepunkt nähern, wird die Genauigkeit der Gompertz-Funktionen recht gut, während die logistische Funktion dazu neigt, Nmax zu unterschätzen.
Bitte beachten Sie, dass alle Modelle davon ausgehen, dass sich die Grundbedingungen im zeitlichen Verlauf nicht ändern und sich ein Prozess wie theoretisch angenommen verhält. Dies ist in der Realität jedoch nicht der Fall, da neue Behandlungen zum Wohle der Menschen die Paramter ändern, eine Verhaltensänderung die Verdopplungszeit einer exponentiellen Infektionskurve ändern kann oder neue Untersuchungsmethoden mehr Infektionen zu Tage bringen. Trotzdem können wir aus allgemeinen Tendenzen viel lernen, wie lange Prozesse dauern und wann wir handeln müssen.
Normalerweise sollten wir bei exponentiellen Problemen so früh wie möglich Handeln. Sehen Sie hier einen Vortrag von Prof. Al Bartlett über das exponentielle Wachstum.
Erweiterte Gompertz Funktion
In der Veröffentlichung am Ende dieser Seite sind einige Vorgängermodelle aufgeführt, die das Verhältnis zwischen den beiden Teilen vor und nach dem Wendepunkt verändern. Die meisten dieser Ansätze funktionieren jedoch bei den Methoden mit dem kleinsten Quadrat nicht einwandfrei und sind nicht stabil im Fit, was bei den zusätzlichen Parametern häufig zu extrem unrealistischen Fehlerwerten führt. Der Grund ist, dass diese Parameter nicht ausreichend unabhängig sind und daher die Anpassung destabilisieren. Hier schlage ich eine andere Methode vor, die diese Probleme kompensiert und stabile Fit ermöglicht:
\[ N(x) = N_{max}\cdot e^{-e^{-(ln(2^{1/w})/(T_2\cdot w^{1/w}))^w\cdot (x^w-d^w)}} \]
In leichter lesbarer Form:
\[ N(x) = N_{max}\cdot e^{-e^-G} \]
\[ G=(\frac{ln(2^{1/w})}{(T_2\cdot w^{1/w})})^w\cdot (x^w-d^w)\]
Der Vorteil dieser Modifikation ist, dass wir alle unsere vorherigen Parameter in ihrer Bedeutung beibehalten, wie die zuvor wichtigen Information: T2 als Verdopplungszeit im Wendepunkt und d als Wendepunkt.
Literatur
.·.